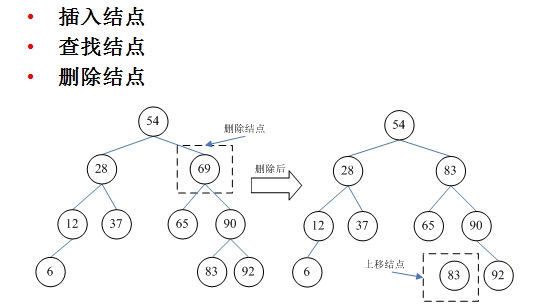
最近查看Java集合類時，有許多用于高效搜索的低級結構，例如哈希，紅黑樹等也被遺忘了二叉排序樹查找算法，因此這只是對Java集合類的系統總結. 搜索相關的結構算法

查找表: 相同類型的數據元素的集合

搜索: 它分為靜態搜索（正義搜索）和動態搜索（包括插入元素和刪除元素）-靜態搜索: 順序搜索（遍歷），半搜索，索引相對簡單，主要分析和分析動態搜索權

二進制搜索樹（BST）是空樹或滿足以下要求的二進制樹:

1. 如果左子樹不為空，則左子樹上任何節點的鍵值小于根節點的鍵值

2. 如果右子樹不為空二叉排序樹查找算法，則右子樹上任何節點的鍵值都大于根節點的鍵值

3. 它的左和右子樹分別是二叉搜索樹

自然

實現Java基本操作

定義BST樹結構如下:

public class BTreeNode {
        int val;//節點的關鍵字值
        BTreeNode left;//左子樹
        BTreeNode right;//右子樹
        BTreeNode(int x) { val = x; }
    }

搜索算法實現

//找到目標值返回該值對應的樹節點，找不到返回null
    public BTreeNode searchBST(BTreeNode node,int des){
        if(node == null)
            return null;
        if(node.val == des)
            return node;
        if(des > node.val)
            return searchBST(node.right,des);
        else
            return searchBST(node.left,des);
    }

搜索時間復雜度分析: 復雜度與BST的樹結構有很大關系. 如果所有節點均按關鍵字遞增或遞減的順序構造，則構造的二叉樹將退化為. 單鏈結構已變為線性復雜度O（n）. 最好的情況是節點盡可能靠近根節點，因此平均和最佳情況下的搜索時間為O（logn），即樹的高度.

插入算法說明

//返回插入元素之后的新的樹結構
    public BTreeNode insertBST(BTreeNode node,int des){
        if(node == null)//如果根節點為空，那么新建一個樹返回
            return new BTreeNode(des);
        if(des == node.val)//如果跟根節點的鍵值等于插入值，那么查找成功，返回原先的樹即可
            return node;
        if(des > node.val)//遞歸調用插入
            node.right = insertBST(node.right,des);
        else
            node.left = insertBST(node.left,des);
        return node;
    }

基本上基于搜索算法，您無需插入找到的元素，只需返回原始樹即可；如果插入的值大于節點的鍵值，則問題將轉換為插入到節點的右子樹中. 其值是關鍵字的節點與小于該值的情況相似，請記住返回結束

刪除算法說明

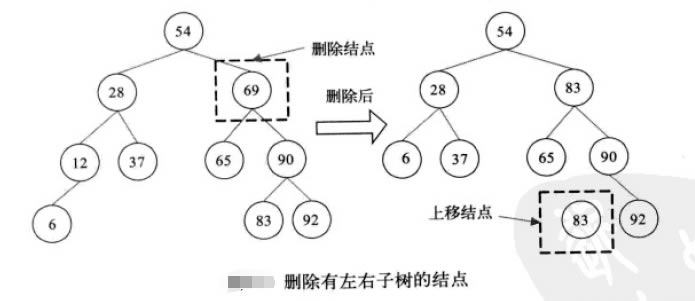
在BST中刪除某個關鍵字的節點，以確保刪除后整個樹結構保持有序，有以下三種刪除情況:

public BTreeNode removeBST(BTreeNode node,int des){
        if(node == null)
            return null;
        if(des == node.val){//查找成功，開始刪除
            if(node.left == null && node.right == null)
                return null;//左右子樹都是空的，直接返回null
            if(node.left == null && node.right != null)
                return node.right;//左子樹為空的時候，右子樹頂點就是新的頭了
            if(node.left != null && node.right == null)
                return node.left;//右子樹為空的時候，左子樹頂點就是新的頭了
            else{//兩個子樹都不為空
                BTreeNode tmp = node.left;
                while(tmp.right != null){
                    tmp = tmp.right;//找到左子樹的最右結點
                }
                node.val = tmp.val;//直接替換值
                node.left = removeBST(node.left,tmp.val);//將左子樹的最有結點刪除
            }
        }
        else if(des > node.val)
            node.right =  removeBST(node.right,des);
        else
            node.left =  removeBST(node.left,des);
        return node;
    }

在實現過程中注意遞歸結束條件，以便當刪除的元素不存在時，它將返回到原始樹結構

本文來自本站，轉載請注明本文網址：
http://www.pc-fly.com/a/jisuanjixue/article-251013-1.html