二進制排序樹是具有以下屬性的空樹或二進制樹:

（1）如果左子樹不為空，則左子樹上所有節點的值小于其根節點的值;

（2）如果右子樹不為空，則右子樹上所有節點的值都大于其根節點的值；

（3）左右子樹也是二進制排序樹；

（4）沒有節點具有相等的鍵值.

如下:

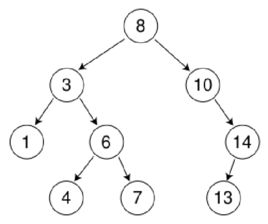
樹遍歷方法通常具有以下方法:

（1）層次遍歷: 按照樹的級別遍歷，如樹所示: 8、3、10、1、6、14、4、7、13

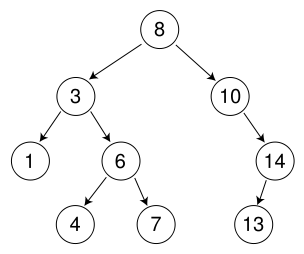
（2）順序遍歷: 節點遍歷順序為當前節點，左節點和右節點. 圖片樹: 8、3、1、6、4、7、10、14、13

（3）中序遍歷: 節點遍歷順序為左節點，當前節點和右節點. 圖片樹: 1、3、4、6、7、8、10、13、14

（4）后續遍歷: 節點遍歷順序為左節點，右節點二叉排序樹的建立，當前節點. 如樹所示: 1，4，7，6，3，8，13二叉排序樹的建立，14，10

package com.lee.wait;
/**
 * Node 二叉樹上的節點
 * @author wait
 *
 */
public class Node {
    /**
     * 節點的數據，這里我們用一個int表示
     */
    public int data;
    /**
     * 節點的左孩子
     */
    public Node left;
    /**
     * 節點的右孩子
     */
    public Node right;
    /**
     * 構造函數，data初始化節點的值
     * @param data
     */
    public Node(int data){
        this.data=data;
    }
    /**
     * 默認構造函數，data=0
     */
    public Node(){
        this(0);
    }
}

（2）二進制排序樹類BTree.java

package com.lee.wait;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
/**
 * BTree二叉排序樹類
 * 
 * @author wait
 * 
 */
public class BTree {
    /**
     * 樹的根節點
     */
    public Node root;
    /**
     * 記錄樹的節點個數
     */
    public int size;
    /**
     * 默認構造函數，樹的根節點為null
     */
    public BTree() {
        root = null;
        size = 0;
    }
    /**
     * 插入一個新的節點node
     * 
     * @param node
     */
    public void insert(Node node) {
        if (root == null) {
            root = node;
            size++;
            return;
        }
        Node current = root;
        while (true) {
            if (node.data <= current.data) {
                // 如果插入節點的值小于當前節點的值，說明應該插入到當前節點左子樹，而此時如果左子樹為空，就直接設置當前節點的左子樹為插入節點。
                if (current.left == null) {
                    current.left = node;
                    size++;
                    return;
                }
                current = current.left;
            } else {
                // 如果插入節點的值大于當前節點的值，說明應該插入到當前節點右子樹，而此時如果右子樹為空，就直接設置當前節點的右子樹為插入節點。
                if (current.right == null) {
                    current.right = node;
                    size++;
                    return;
                }
                current = current.right;
            }
        }
    }
    /**
     * 插入一個值為data的節點
     * 
     * @param data
     */
    public void insert(int data) {
        insert(new Node(data));
    }
    /**
     * 根據int數組里面的值建立一個二叉排序樹
     * 
     * @param datas
     */
    public void bulidTree(int[] datas) {
        for (int i = 0, len = datas.length; i < len; i++) {
            insert(datas[i]);
        }
    }
    /**
     * 返回二叉排序樹的層次遍歷的結果，使用通用的廣度優先遍歷方法
     * 
     * @return 以int數組的形式返回結果
     */
    public int[] layerOrder() {
        int[] res = new int[size];
        if (root == null) {
            return res;
        }
        // 用一個隊列存儲節點的順序，一次放入根節點，根的左孩子節點，根的右孩子節點
        Queue<Node> queue = new LinkedList<Node>();
        queue.offer(root);
        int i = 0;
        while (!queue.isEmpty()) {
            Node current = queue.poll();
            res[i++] = current.data;
            if (current.left != null) {
                queue.offer(current.left);
            }
            if (current.right != null) {
                queue.offer(current.right);
            }
        }
        return res;
    }
    /**
     * 先序遍歷二叉排序樹，非遞歸的方法，深度優先思想
     * 
     * @return 以int數組的形式返回結果
     */
    public int[] preOrder() {
        int[] res = new int[size];
        int i = 0;
        //使用stack存儲遍歷到的節點
        Stack<Node> stack = new Stack<Node>();
        Node node = root;
        while (node != null) {
            //一直往下遍歷，知道到左孩子節點為空
            while (node != null) {
                stack.push(node);
                res[i++] = node.data;
                node = node.left;
            }
            //左孩子節點為空之后，往后找，如果找到的上一個節點的右孩子節點為空，那么繼續往上找，直到找到一個右孩子節點不為空的
            while (!stack.isEmpty() && stack.peek().right == null) {
                node = stack.pop();
            }
            if(!stack.isEmpty()){
                node=stack.pop();
                //找到了一個右孩子節點不為空的節點，就去遍歷他的右孩子節點
                if (node != null) {
                    node = node.right;
                }
            }else{
                node=null;
            }
        }
        return res;
    }
    /**
     * 中序遍歷二叉排序樹  非遞歸的方法，深度優先思想
     * @return
     */
    public int[] inOrder() {
        int[] res = new int[size];
        int i = 0;
        //使用stack存儲遍歷到的節點
        Stack<Node> stack = new Stack<Node>();
        Node node = root;
        while (node != null) {
            //一直往下遍歷，知道到左孩子節點為空
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            //左孩子節點為空之后，往后找，找到上一個節點.如果找到的上一個節點的右孩子節點為空，那么繼續往上找，直到找到一個右孩子節點不為空的
            while (!stack.isEmpty() && stack.peek().right == null) {
                node = stack.pop();
                res[i++] = node.data;
            }
            if (!stack.isEmpty()) {
                node = stack.pop();
                res[i++] = node.data;
                //找到了一個右孩子節點不為空的節點，就去遍歷他的右孩子節點
                if (node != null) {
                    node = node.right;
                }
            }else{
                node=null;
            }
        }
        return res;
    }
    /**
     * 后序遍歷二叉排序樹  非遞歸的方法，深度優先思想
     * @return
     */
    public int[] postOrder() {
        int[] res = new int[size];
        int i = 0;
        //使用stack存儲遍歷到的節點
        Stack<Node> stack = new Stack<Node>();
        Node node = root;
        //存儲每個節點是否訪問被回訪過，也就是是否是從左子樹還是右子樹回訪的。
        Stack<Boolean> stackFlag=new Stack<Boolean>();
        while (node != null) {
            //一直往下遍歷，知道到左孩子節點為空
            while (node != null) {
                stack.push(node);
                stackFlag.add(false);
                node = node.left;
            }
            //左孩子節點為空之后，往后找，找到上一個節點.如果找到的上一個節點的右孩子節點為空，那么繼續往上找，直到找到一個右孩子節點不為空的
            while (!stack.isEmpty() && (stack.peek().right == null||stackFlag.peek()==true)) {
                node = stack.pop();
                stackFlag.pop();
                res[i++] = node.data;
            }
            if (!stack.isEmpty()) {
                node=stack.peek();
                stackFlag.pop();
                stackFlag.add(true);
                //找到了一個右孩子節點不為空的節點，就去遍歷他的右孩子節點
                if (node != null) {
                    node = node.right;
                }
            }else{
                node=null;
            }
        }
        return res;
    }
    /**
     * 先序遍歷，遞歸方法實現
     * @param node 當前訪問的節點
     * @param list 存儲節點值的容器
     */
    private void preOrderRe(Node node,List<Integer> list){
        if(list==null){
            list=new ArrayList<>();
        }
        if(node==null){
            return;
        }
        list.add(node.data);
        if(node.left!=null){
            preOrderRe(node.left,list);
        }
        if(node.right!=null){
            preOrderRe(node.right,list);
        }
    }
    /**
     * 先序遍歷，遞歸 調用上面實現函數
     * @return
     */
    public int[] preOrderRe(){
        List<Integer> list = new ArrayList<>();
        preOrderRe(root, list);
        int[] res=new int[size];
        for(int i=0,size=list.size();i<size;i++){
            res[i]=list.get(i);
        }
        return res;
    }
    /**
     * 中序遍歷，遞歸方法實現
     * @param node 當前訪問的節點
     * @param list 存儲節點值的容器
     */
    private void inOrderRe(Node node,List<Integer> list){
        if(list==null){
            list=new ArrayList<>();
        }
        if(node==null){
            return;
        }
        if(node.left!=null){
            inOrderRe(node.left,list);
        }
        list.add(node.data);
        if(node.right!=null){
            inOrderRe(node.right,list);
        }
    }
    /**
     * 中序遍歷，遞歸 調用上面實現函數
     * @return
     */
    public int[] inOrderRe(){
        List<Integer> list = new ArrayList<>();
        inOrderRe(root, list);
        int[] res=new int[size];
        for(int i=0,size=list.size();i<size;i++){
            res[i]=list.get(i);
        }
        return res;
    }
    /**
     * 后序遍歷，遞歸方法實現
     * @param node 當前訪問的節點
     * @param list 存儲節點值的容器
     */
    private void postOrderRe(Node node,List<Integer> list){
        if(list==null){
            list=new ArrayList<>();
        }
        if(node==null){
            return;
        }
        if(node.left!=null){
            postOrderRe(node.left,list);
        }
        if(node.right!=null){
            postOrderRe(node.right,list);
        }
        list.add(node.data);
    }
    /**
     * 后序遍歷，遞歸 調用上面實現函數
     * @return
     */
    public int[] postOrderRe(){
        List<Integer> list = new ArrayList<>();
        postOrderRe(root, list);
        int[] res=new int[size];
        for(int i=0,size=list.size();i<size;i++){
            res[i]=list.get(i);
        }
        return res;
    }
}

（3）測試代碼TestBTree.java

本文來自本站，轉載請注明本文網址：
http://www.pc-fly.com/a/jisuanjixue/article-252817-1.html