| 根據運行的環境,操作系統可以分為桌面操作系統,手機操作系統,服務器操作系統,嵌入式操作系統等。 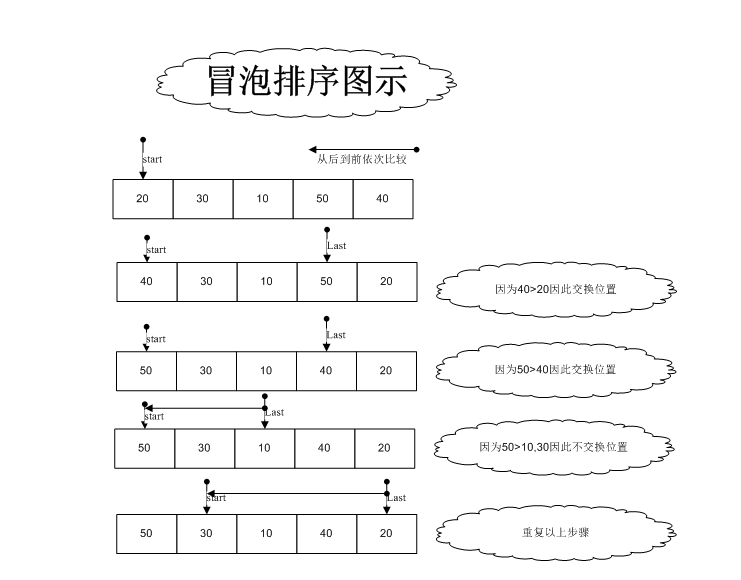
以下是每個數據結構的詳細介紹. 對于每種數據結構,它將主要從JS的角度列出經常遇到的經典問題和實現方法,但是只要思路清楚,使用哪種語言,對于本文來說就不那么重要了
對于數組,它是Wuli中程序員最熟悉的數據結構. 我仍然記得當我還是學生時比較數組和鏈接列表.
最受關注的是兩點: 查詢和插入刪除. 當需要高頻率插入和刪除時,選擇鏈表;當您需要高頻查詢時,選擇數組.
數組插入和刪除: 要插入和刪除項目,首先需要找到滿足特定條件的位置,然后在插入和刪除項目時,需要移動所有其他項目,以便可以清空或填充插入和刪除位置,這樣您就可以動員除了所有項目之外,這些操作的執行頻率很高,而且性能遠不及直接修改下一個列表. 鏈表查詢: 如果要查詢特定位置的節點,則需要從頭節點開始依次遍歷;并且數組具有下標,則可以直接訪問下標的項. 在數組中找到第k個最小元素
使用快速排序的想法,left [](<)right [],從小到大排序,如果m="">
實現:
var kArr = function(arr,k){
if(arr.length < k){console.log("沒有這么多數呀!");return}
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
if(left.length<k){
return right[k-left.length];
}
else{
return left[k];
}
}
var arr = [1,3,2,5,11,43,22,77,45,12];
console.log(kArr(arr,6));
復制代碼
找到第一個沒有重復的數組元素
實現: (1)用兩層循環直接掃描數組(2),用map計算每個元素val的出現次數,然后返回val為1的第一項.
談到上面的第二種方法,作者凍結了一些. 在加入秋季技巧之前,面試女士問了一個簡單的算法問題,并問我進行了哪些優化. 當時我以為這很復雜,我完全沒有去做. 受試者認為c語言單鏈表冒泡排序,哭泣和流鼻涕,仍然需要回答問題以找到感覺-.-
//查找第一個沒有重復的元素
var oneArr = function(arr){
if(arr.length === 1){return arr[0]};
var obj = {};
arr.forEach(element => {
if(!obj[element]) obj[element] = 1;
else obj[element]++;
});
for(var key in obj){
if(obj[key] === 1) {
return key;
}
}
}
var arr = [1,3,2,5,11,3,22,77,45,1,77,0,0];
console.log(oneArr(arr));
復制代碼
合并兩個排序的數組
實現:
由于JS的實現非常簡單,只需在concat之后直接排序,如果不使用這些方法,則可以使用兩個指針指向兩個數組,讓兩個元素進行比較,將其中的小元素放入新數組中,并將較小元素的數組指針增加1,并繼續進行比較,直到遍歷一個數組為止. 最后,將另一個數組的其余元素放入新數組.

重新排列數組中的正數和負數
實現:
使用快速排序的思想,將整數和負數分別放在right []和left []中,然后分別對它們進行排序,最后進行合并
堆棧的主要核心: 先進;堆棧是一種特殊的線性表,只能性表的一端進行操作,允許堆棧的頂部進行操作,而不允許堆棧的底部進行操作.
遞歸函數的實現利用堆棧數據結構. 調用遞歸函數時,局部變量,形式參數值和被調用函數的返回地址都存儲在遞歸工作堆棧中. 該函數將在運行時按照后進先出的順序執行,以完成遞歸操作.
根據編譯原理,我們使用堆棧的結構特征來計算后綴表達式.
示例: 中綴表達式a + b * c +(d * e + f)* g,轉換為后綴表達式后為a b c * + d e * f + g * +
特定的轉換過程:
1)如果遇到操作數,請直接輸出
2)如果遇到運算符,則將其放在堆棧上,并將左括號也放在堆棧上
3)如果遇到右括號,將彈出堆棧元素,并且將輸出彈出的運算符,直到遇到左括號為止. 左括號只會彈出而不會輸出
4)其他運算符,例如+,*,(從堆棧中彈出元素,直到遇到優先級較低的元素或空堆棧. 彈出這些元素后,只能將遇到的運算符按入棧,這很重要請注意,它只會在遇到時彈出(在其他情況下不會彈出)
5)如果讀取了輸入的結尾,則將按順序彈出堆棧中的所有元素
實現: 首先通過js-class實現堆棧結構,然后使用輔助堆棧幫助實現堆棧堆棧排序

class Vect{
constructor(){
this.stack = [];
}
//入棧
in(num){
if (typeof num != "number") return false;
this.stack.push(num);
}
//出棧
out(){
if(this.stack.length>0){
let last = this.stack.pop();
return last;
}
}
//輸出
print(){
if(this.stack.length === 0){
console.log("棧空了");
}
else{
console.log(...this.stack);
}
}
}
//利用輔助棧對存儲棧排序
var sort = function(stack){
var help = new Vect();
while(stack.stack.length){
var pop = stack.out();
if(help.stack.length&&help.stack[help.stack.length-1]<pop) {//里面的判斷順序不能顛倒,否則出現 java.util.EmptyStackException
stack.in(help.out());//當滿足help不為空,且help的元素小于pop(這樣排出的順序頂到底是從小到大的)
} //將help里的元素返回到stack中
help.in(pop);//無論什么情況,只要stack不為空,都將pop壓入help
}
while(help.stack.length) {//當help不為空的時候,help里面的元素頂到底是從小到大的,
stack.in(help.out());//所以將help彈到stack中是頂到底是從大到小的
}
stack.print();
}
var stack = new Vect();
stack.in(2);
stack.in(1);
stack.in(5);
sort(stack);
復制代碼
詳細的排序過程:
進入堆棧[2,1,5],創建空堆棧helpstack pop pop = 5,因為此時幫助為空,直接在幫助堆棧中,然后pop pop = 1,因為1 <5,直接進入幫助堆棧(確保幫助堆棧是從上到下的: 大-小),然后在堆棧上彈出pop="2,因為1"><2,將pop =="" 1在幫助中直接放入堆棧,然后將2放入堆棧繼續堆棧,堆棧會彈出pop="">c語言單鏈表冒泡排序,因為2> 1,直接在幫助堆棧中,最后將所有幫助彈出到堆棧中,即有序生成堆棧.
幫助堆棧
堆棧堆棧
為簡單起見,我們直接判斷()是否匹配,如果需要其他符號,我們可以添加判斷
實現思路:
在實現過程中,默認值為“(“”“)”,如果第一件事遇到“)”,它將直接跳出,顯示“還有更多右括號”.
掃描str遇到“(”,堆棧遇到“)”,判斷堆棧,如果為空,則有更多右括號,返回false;如果不為空,則判斷頂部堆棧的頂部,如果不為左括號,則不匹配,返回false;否則,返回false. 如果是左括號,則退出堆棧,繼續下一次掃描,確定堆棧是否為空,如果不為空,則表示左括號不匹配,左括號更多,返回false;否則,返回false. 否則匹配成功,返回true
var match = function(str){
var strStack = new Vect();
var strArr = str.split('');
var p = 0;
while(p<strArr.length){
if(strArr[p]==="("){
strStack.in(strArr[p]);
}
if(strArr[p]===")"){
if(strStack.stack.length===0){
console.log("右括號多了");
return false;
}
else if(strStack.stack[strStack.stack.length-1]!=="("){
console.log("不匹配");
return false;;
}
else{
strStack.out();
}
}
p++;
}
if(strStack.stack.length){
console.log("左括號多于右括號");
return false;
}
else{
console.log("左右括號匹配正確");
return true;
}
}
match("((a+b)*v)/2)");
復制代碼
隊列與堆棧相反. 核心是先進先出. 實現方法類似于堆棧. 區別在于入隊和出隊的順序.
鏈表是由節點和下一個連接的鏈. 在本文中,我們將簡要介紹單鏈表結構的實現以及相關問題的實現
JS實現單個鏈表的結構,并實現鏈表的添加,刪除,搜索和反向
class Node{
constructor(element){
this.element = element;
this.next = null;
}
}
class LinkedList{
constructor(){
this.length = 0;
this.head = null;
}
append(element){
let node = new Node(element);
let current;
if(this.head == null) this.head = node;
else{
current = this.head;
while(current.next){
current = current.next;
}
current.next = node;
}
this.length++;
}
removeAt(position){
if(position >-1 && position < this.length){
let current = this.head;
let index = 0;
let previous;
if(position == 0){
this.head = current.next;
}else{
while(index++ < position){
previous = current;
current= current.next;
}
previous.next = current.next;
}
this.length--;
return current.element;
}
else{
return null;
}
}
insert(position,element){ //插入
if(position >-1 && position <= this.length){
let node = new Node(element);
let current = this.head;
let index = 0;
let previous;
if(position==0){
node.next = current;
this.head = node;
}else{
while(index++<position){
previous = current;
current = current.next;
}
previous.next = node;
node.next = current;
}
this.length++;
return true;
}else{
return false;
}
}
toString(){ //轉成字符串
let current = this.head;
let str = '';
while(current){
str += ','+current.element;
current = current.next;
}
return str;
}
indexOf(element){ //索引
let current = this.head;
let index = 0;
while(current){
if(current.element == element){
return index;
}
index++;
current = current.next;
}
return -1;
}
reverse(){ //反轉
if(this.head === null || this.head.next===null) return;
let current = this.head;
let pnext = current.next;
current.next = null;
while(pnext){
let pp = pnext.next;
pnext.next = current;
current = pnext;
pnext = pp;
}
this.head = current;
}
}
let link = new LinkedList();
link.append("111");
link.append("222");
link.append("333");
link.reverse();
console.log(link);
console.log(link.indexOf("111"));
復制代碼

相反的結果:
檢查鏈表中是否有循環返回鏈表的倒數第二個元素以刪除鏈表中的重復元素
說明: 圖由一組有限的頂點和一組頂點之間的邊組成,通常表示為: G(V,E),其中G表示圖,而V在圖G中. 是圖G中的一組邊. 圖中的數據元素稱為頂點,而該頂點集是無限非空的. 在圖中,任何兩個頂點之間可能存在關系. 頂點之間的邏輯關系由邊表示,并且邊集可能為空.
確定圖是否為樹: 確保圖已連接,并且圖沒有環
(1)是否有環: 兩個數組,一個二維數組作為圖的鄰接矩陣,一個一維數組,用于標記是否已遍歷一個節點(2)是否已連接: 檢查上面的一維數組是否具有遍歷
統計圖中的邊數,n個節點: 完全有向圖n(n-1),完全無向圖n(n-1)/ 2
N二叉樹,平衡樹,二叉樹,二叉搜索樹,平衡二叉樹,紅色和黑色樹,B樹
摘要:
具有n個節點的二叉樹,分支樹為n-1. 如果二叉樹的高度為h,則至少有h個節點,并且最多2 ^ h -1個節點(完整的二叉樹). 具有n個節點的二叉樹,高度最大n,最小高度log2(n + 1)向上舍入一個具有n個節點的完整二叉樹,高度height log2(n + 1)向上舍入一個Huffman樹: 權重最小的二叉樹
非葉??節點的最大數量為兩個子節點;左子節點小于右子節點;左右邊之差不超過1;沒有相同的重復節點
紅黑樹也是平衡的二叉樹
排序算法,這是四個主要細節,描述了作者的個人理解,并且將來會繼續覆蓋其他內容
算法算法
如何定義穩定和不穩定的排序算法?
(1)穩定: 排序前b之前a,a = b,排序后b之前a靜止(冒泡,插入,合并,基數)(2)不穩定: 排序前a之前b之前,a = b,排序后,a可能在b(select,fast,hill,heap)之后
以下按從小到大的順序分析了各種實現:
從數組中的第一個數字開始,然后依次遍歷數組中的每個數字. 通過相鄰的比較交換,每輪循環都會找到最大數量的剩余未排序數字,并在數組“最后一個”中“冒泡”.
//冒泡
for(i=0;i<len-1;i++){
for(j=0;j<len-1-i;j++){//每一輪最后一個元素都是最值,所以可以不用再比
if(arr[j]>arr[j+1]){
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
復制代碼
從所有記錄中選擇最小的數據元素,以便與第一個位置的記錄進行交換;然后在剩余記錄中找到最小的交換,并將記錄放在第二個位置,循環直到只有最后一個保留Data元素.
//選擇
for(i=0;i<len-1;i++){
var minIndex = i;
for(j=i+1;j<len;j++){
if(arr[j]<arr[minIndex]){
minIndex = j;
}
}
var temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
復制代碼
從要排序的n條記錄中的第二條記錄開始,然后依次與前一條記錄進行比較以找到插入位置. 每個外循環結束后,將當前編號插入適當的位置.
//插入
for(i=1;i<len;i++){
if(arr[i]<arr[i-1]){
var temp = arr[i];
var j = i-1;
while(j>=0 && temp<arr[j]){
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}
復制代碼
插入排序的優化: 當我們找到要插入的位置時,我們可以使用二進制搜索來找到位置
// 優化(二分查找)
for(var i = 1;i<len;i++){
var key = arr[i];
var j = i-1;
var right = i-1;
var left = 0;
while(left<=right){
var mid = parseInt((left+right)/2);
if(key<arr[mid]){
right = mid-1;
}
else{
left = mid+1;
}
}
// 這里最終找到的是left
for(var j=i+1;j>=left;j--){
arr[j+1] = arr[j];
}
arr[left] = key;
}
復制代碼
從序列中選擇一個元素作為引用,并左右創建兩個數組,將小于引用的元素放在左側,將大于引用的元素放在右側,然后遞歸,最后連接兩個數組get是排序后的數組.
var quickSort2 = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort2(left).concat([pivot], quickSort2(right));
};
復制代碼
里面有些內容還沒有補充,持續整理更新。。。有錯誤請指教,共同進步
復制代碼
轉載于:
本文來自本站,轉載請注明本文網址:
http://www.pc-fly.com/a/jisuanjixue/article-259602-1.html
| 
