| 根據運行的環境,操作系統可以分為桌面操作系統,手機操作系統,服務器操作系統,嵌入式操作系統等。 
最近回顧了C ++語言,在回顧過程中,我順便回顧了數據結構的某些內容,用一顆石頭殺死了兩只鳥!以下是用于實現二進制排序樹的類模板.
首先定義節點類型和二叉樹類型:
template<typename T>
class BinaryTree;
template<typename T> //節點類的定義
class Node
{private:
Node<T>*lchild, *rchild;
T info;
public:
Node()
{
lchild = NULL;
rchild = NULL;
}
Node(T data, Node<T>*left = NULL, Node<T>*right = NULL)
{
info = data;
lchild = left;
rchild = right;
}
friend class BinaryTree < T > ;
};
template<typename T> //二叉排序樹類的定義
class BinaryTree
{
Node<T>*root;
void Inorder(Node<T>*current);
void Insert(const T &data,Node<T>* &b);
void Remove(const T &data, Node<T>* &a, Node<T>* &b);
void Destory(Node<T>*current); //刪除二叉排序樹
public:
BinaryTree(){ root = NULL; }
~BinaryTree(){ Destory(root); }
void Create(T*data, int n); //由數組創建二叉排序樹,n是數組大小
void InOrder(){ Inorder(root); } //中序遍歷
void Remove(const T&data){ Remove(data,root,root); } //刪除節點
};
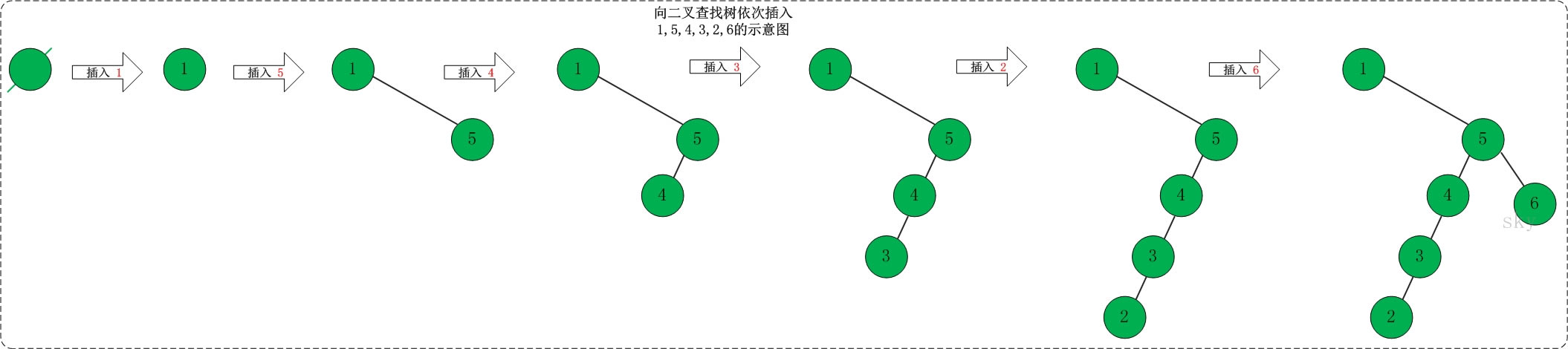
上面定義的二進制排序樹類中涉及一些簡單的操作:
template<typename T>
void BinaryTree<T>::Insert(const T &data, Node<T>* &b) //遞歸法在二叉排序樹中插入一個節點
{
if (b == NULL) //遞歸終止條件
{
b = new Node<T>(data);
if (!b)
{
cout << "out of space!" << endl;
}
}
else if (data < b->info)
Insert(data, b->lchild);
else
Insert(data, b->rchild);
}
template<typename T>
void BinaryTree<T>::Inorder(Node<T>*current) //中序遍歷
{
if (current != NULL)
{
Inorder(current->lchild);
cout << current->info<<" ";
Inorder(current->rchild);
}
}
template<typename T>
void BinaryTree<T>::Create(T*data, int n) //由數組創建二叉排序樹,n是數組大小
{
for (int i = 0; i < n; i++)
{
Insert(data[i],root);
}
}
對于二進制排序樹的相關操作,我個人認為最技術上的內容是刪除節點. 在這個問題上還有更多的案例需要考慮.
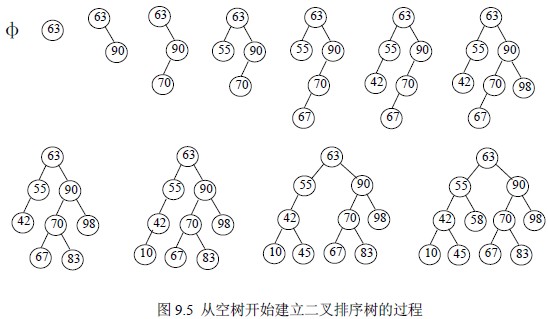
刪除節點需要考慮相應節點的狀態,特別是該節點是否為空,如果不為空,則其左右子樹是否存在. 我們可以進行如下操作:
1. 要找到要刪除的節點,您需要在搜索時記錄要刪除的節點的父節點c++二叉排序樹,因為需要同時清理該節點(空白節點的父子節點或子節點).
2. 根據待刪除節點左右子樹的狀態,進行相應的處理,這些狀態包括:
1. 如果要刪除的節點的左右節點不存在,則將其直接刪除,并清空其父節點(如果有父節點)的相應指針.
2. 如果要刪除的節點的左子樹存在,則右子樹不存在,或者左子樹不存在,并且右子樹存在. 只需直接在其子樹中添加一個候選邊即可.
3. 如果存在要刪除的節點的左右子樹,則情況會稍微復雜一些. 必須根據二進制排序樹的性質,從左側的子樹或子樹中選擇節點以填充要刪除的節點的位置.
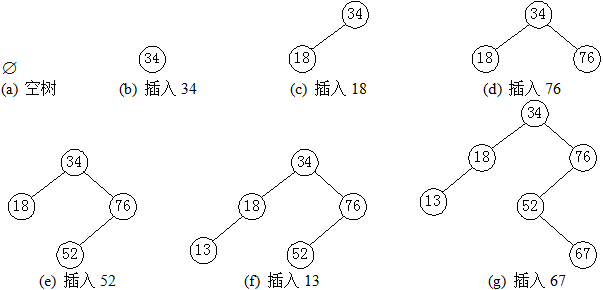
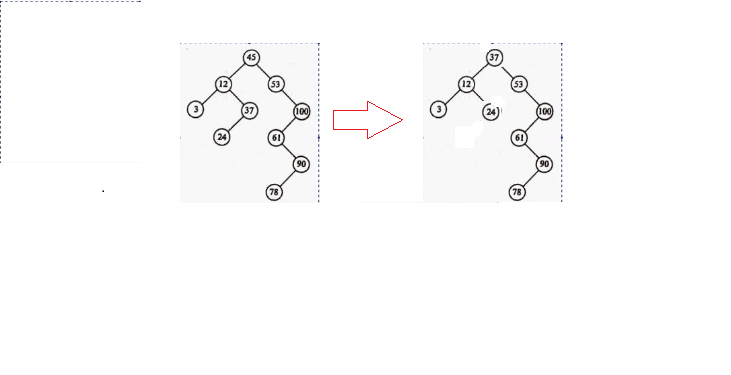
通常,在樹的中間遍歷中與要刪除的節點相鄰的節點(左和右節點都可以c++二叉排序樹,這里是右節點值)來替換要刪除的節點. 實際執行刪除操作時,不會
真正刪除要刪除的節點,但是將要刪除的節點的鍵值分配給替換節點的鍵值,然后刪除替換節點.
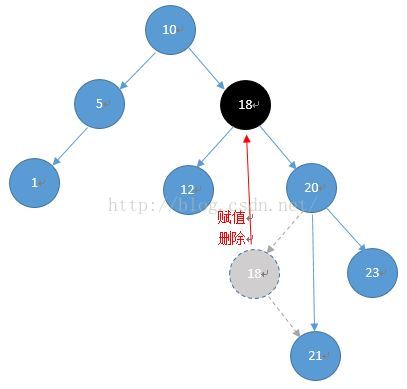
(a)(b)
上圖(a)至(b)是典型的刪除過程,其中要刪除的節點的左右子樹都存在: 要刪除15個節點,請首先將21個節點更改為20個左邊的子樹節點,然后更改18個節點. 請參閱將值復數值更改為要刪除的15個節點,最后刪除原始的18個節點.
template<typename T>
void BinaryTree<T>::Remove(const T &data, Node<T>* &a, Node<T>* &b)
{
Node<T>*temp1, *temp2;
if (b == NULL) { cerr << "Invalid input"; return; }
if (data < b->info) Remove(data, b, b->lchild); //先找到節點位置,這里沒有考慮找不到的情況
else if (data >b->info) Remove(data, b, b->rchild);
?else if (b->lchild != NULL&&b->rchild != NULL) //這個分支以及下面的分支表示已找到data所在節點
{
temp2 = b;
temp1 = b->rchild;
if (temp1->lchild != NULL)
{
while (temp1->lchild != NULL)
{
temp2 = temp1;
temp1 = temp1->lchild;
}
temp2->lchild = temp1->rchild;
}
else temp2->rchild = temp1->rchild;
b->info = temp1->info;
delete temp1;
}
else //左右子樹中至少有一個不存在的情況
{
temp1 = b;
if (b->rchild != NULL)
{
temp1 = b->rchild;
b->info = temp1->info;
b->rchild = temp1->rchild;
b->lchild = temp1->lchild;
}
else if (b->lchild != NULL)
{
temp1 = b->lchild;
b->info = temp1->info;
b->rchild = temp1->rchild;
b->lchild = temp1->lchild;
}
else if (b == root) root = NULL;
else if (a->rchild == temp1) a->rchild = NULL;
else a->lchild = NULL;
delete temp1;
}
}
以上代碼已經過測試并通過,歡迎交流.
本文來自本站,轉載請注明本文網址:
http://www.pc-fly.com/a/jisuanjixue/article-286414-1.html
| 
